Definition 6 (Divisor, Divisorengruppe, Grad)
Die
Divisorengruppe
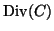
einer Kurve
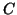
ist die von
den Punkten erzeugte freie abelsche Gruppe, d.h. ein
Divisor
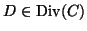
ist eine formale Summe
mit
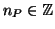
und
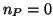
für fast alle
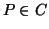
.
Der Grad von 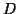 ist definiert als
ist definiert als
Definition 7 (Hauptdivisor)
Ein Divisor ist ein
Hauptdivisor, wenn er die Form
mit einer rationalen Funktion (in diesem Fall ,,Polynom durch
Polynom``)
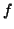
besitzt.
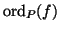
bezeichnet hierbei die
Nullstellenordnung der Funktion
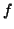
am Punkt
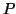
.
Definition 8 (lineare Äquivalenz von Divisoren)
Zwei Divisoren
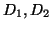
heißen
linear äquivalent, wenn
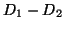
ein Hauptdivisor ist.
Definition 9 (Divisoren von Grad
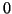
)
Die Gruppe
bezeichnen wir als
Gruppe der Divisoren von Grad 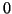
, sie
enthält also die Divisoren, deren Koeffizienten sich zu
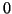
addieren
und bildet eine Untergruppe von
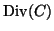
.
Definition 10 (Divisorenklassengruppe)
Die
Divisorenklassengruppe (oder
Picard-Gruppe)
von 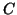
, bezeichnet mit
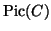
ist der Quotient von
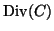
durch die Untergruppe der Hauptdivisoren.
Der Grad 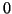 -Teil der Divisorenklassengruppen von
-Teil der Divisorenklassengruppen von 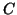 ,
bezeichnet
,
bezeichnet
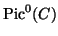 ist der Quotient von
ist der Quotient von
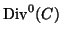 durch die
Untergruppe der Hauptdivisoren.
durch die
Untergruppe der Hauptdivisoren.
Eine elliptische Kurve 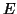 ist isomorph zum Grad
ist isomorph zum Grad 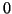 -Teil der
Divisorenklassengruppe, wobei ein Punkt
-Teil der
Divisorenklassengruppe, wobei ein Punkt 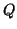 einem Divisor
einem Divisor
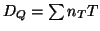 entspricht, wenn
entspricht, wenn 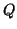 in
in 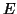 eine Summe der Punkte
eine Summe der Punkte 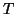 mit
Vielfachheit
mit
Vielfachheit 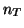 ist. Ist ferner
ist. Ist ferner
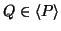 , dann ist
, dann ist 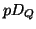 ein
Hauptdivisor, geschrieben
ein
Hauptdivisor, geschrieben 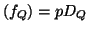 für eine Funktion
für eine Funktion 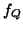 auf
auf 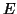 .
.
Stefan Röhrich stefan@roehri.ch
2002-04-23 21:32:56
![]() ist definiert als
ist definiert als
![]() -Teil der Divisorenklassengruppen von
-Teil der Divisorenklassengruppen von ![]() ,
bezeichnet
,
bezeichnet
![]() ist der Quotient von
ist der Quotient von
![]() durch die
Untergruppe der Hauptdivisoren.
durch die
Untergruppe der Hauptdivisoren.![]() ist isomorph zum Grad
ist isomorph zum Grad ![]() -Teil der
Divisorenklassengruppe, wobei ein Punkt
-Teil der
Divisorenklassengruppe, wobei ein Punkt ![]() einem Divisor
einem Divisor
![]() entspricht, wenn
entspricht, wenn ![]() in
in ![]() eine Summe der Punkte
eine Summe der Punkte ![]() mit
Vielfachheit
mit
Vielfachheit ![]() ist. Ist ferner
ist. Ist ferner
![]() , dann ist
, dann ist ![]() ein
Hauptdivisor, geschrieben
ein
Hauptdivisor, geschrieben ![]() für eine Funktion
für eine Funktion ![]() auf
auf ![]() .
.