Nächste Seite: Details Aufwärts: Funktionsweise Vorherige Seite: Divisoren Inhalt
Wir definieren mit einem festen Punkt
![]() :
:
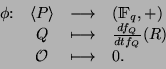
Für
![]() ist diese Abbildung wohldefiniert
(Beweis folgt in Lemma 2), in diesem Fall ist
ist diese Abbildung wohldefiniert
(Beweis folgt in Lemma 2), in diesem Fall ist ![]() ein
injektiver Homomorphismus.
ein
injektiver Homomorphismus.
![]() läßt sich durch eine rekursive
Zerlegung berechnen (Details siehe Beweis von Lemma
3), bei dieser Zerlegung mit Tiefe
läßt sich durch eine rekursive
Zerlegung berechnen (Details siehe Beweis von Lemma
3), bei dieser Zerlegung mit Tiefe ![]() treten
pro Zerlegungsschritt nur konstant viele neue Elemente auf, wobei die
Berechnungen in einer Körpererweiterung von
treten
pro Zerlegungsschritt nur konstant viele neue Elemente auf, wobei die
Berechnungen in einer Körpererweiterung von ![]() von maximal Grad
3 durchgeführt werden können.
von maximal Grad
3 durchgeführt werden können.
Somit läßt sich ![]() in
in ![]() Schritten berechnen, d.h. der
Aufwand zur Berechnung des diskreten Logarithmus ist in unserem Fall
polynomial in der Bitlänge des zugrundeliegenden Körpers.
Schritten berechnen, d.h. der
Aufwand zur Berechnung des diskreten Logarithmus ist in unserem Fall
polynomial in der Bitlänge des zugrundeliegenden Körpers.