Als nächsten wichtigen Schritt führen wir nun die diskrete
Fouriertransformation ![]() auf unserem ersten Register aus, die
auf unserem ersten Register aus, die
![]() (
(![]() ) wie folgt abbildet:
) wie folgt abbildet:
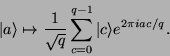 |
(15) |
Das heißt, wir wenden die unitäre Abbildung auf ![]() an, die der
Matrix mit den
an, die der
Matrix mit den ![]() -Einträgen
-Einträgen
![]() entspricht. Diese Transformation ist auf einem Quantencomputer
effizient durchführbar (
entspricht. Diese Transformation ist auf einem Quantencomputer
effizient durchführbar (
![]() in
in ![]() möglich, im
Gegensatz dazu benötigt man dabei auf einem klassischen Computer
mittels der Fast Fourier Transformation
möglich, im
Gegensatz dazu benötigt man dabei auf einem klassischen Computer
mittels der Fast Fourier Transformation ![]() Schritte) und Thema
eines eigenen Vortrages.
Schritte) und Thema
eines eigenen Vortrages.
Wir erhalten nun den folgenden Zustand:
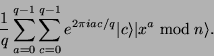 |
(16) |