Modulare Exponentation

Unsere Transformationen bei einem Quantencomputer müssen unitär, also insbesondere reversibel sein, deshalb führen wir unseren Eingabewert $a$ einfach in einem zusätzlichen Register weiterhin mit und legen den Funktionswert in einem weiteren, vorher nur mit $\vert\rangle$ belegtem Register ab:

$$\vert a\rangle \vert\rangle \mapsto \vert a\rangle \vert x^a \bmod n\rangle .$$ (13)

Die Modulare Exponentation ist effizient durchführbar, z.B. mittels Square-and-Multiply und Schönhage-Strassen für die dabei auftretenden Multiplikationen mit $O(l^2 \log l \log \log l)$ Zeit- und $O(l \log l \log \log l)$ Speicheraufwand oder mit ,,gewöhnlicher`` Multiplikation mit einem Aufwand von $O(l^3)$ an Zeit und $O(l)$ an Speicher ($l$ bezeichnet hierbei eine $l$-Bit-Zahl). Trotzdem stellt sie die langsamste Operation des Faktorisierungsalgorithmus dar. Allerdings ist es interessant, daß der Schönhage-Strassen-Multiplikationsalgorithmus die schnelle Fourier-Transformation benutzt, die die Grundlage für viele Quantenalgorithmen darstellt. So ist es vielleicht denkbar, daß dadurch sogar die Ganzzahl-Multiplikation auf einem Quantencomputer beschleunigt werden könnte, was zu einem besseren asymptotischem Verhalten des Quantenfaktorisierungsalgorithmus führen würde und u.U. sogar das Brechen von RSA auf einem Quantencomputer asymptotisch schneller machen könnte als die RSA-Verschlüsselung auf einem klassischen Computer (näheres zur schnellen Implementation des Shor-Algorithmus wird in [Zal98] geschildert, dort findet sich auch eine Variante, die die FFT zur Multiplikation verwendet).

Diese klassischen Algorithmen lassen sich als Quantengatter realisieren, wobei darauf geachtet werde muß, daß die verwendeten Operationen reversibel sind. Insbesondere muß dabei ein Zwischenspeicher wieder auf $0$ gesetzt werden, dies kann aber nicht direkt geschehen, sondern kann nur über einen Umweg erreicht werden. Um nun zu überprüfen, ob die bisherige Rechnung korrekt war, kann man nun diesen Zwischenspeicher messen, wird ein Wert ungleich $0$ gemessen, wiederholt man die Rechnung, anderenfalls ist man zudem sicher, daß jede Amplitude ungleich $0$ durch die Messung zerstört wurde und kann somit u.U. sogar die Genauigkeit erhöhen. Diese Methode heißt ,,quantum watchdog``- oder auch ,,quantum Zeno``-Effekt. Da die Messung aber auch einen Aufwand darstellt, müßte noch getestet werden, ob der Gewinn an Genauigkeit an dieser Stelle eine Geschwindigkeitsverbesserung des gesamten Algorithmus bewirkt.

Man erhält nun folgenden Zustand nach Anwendung der Funktion:

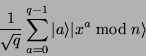$$\frac{1}{\sqrt{q}} \sum_{a=0}^{q-1} \vert a\rangle \vert x^a \bmod n\rangle$$ (14)

Abbildung: Beispiel eines Funktionsgraphen der modulo-Exponentation für $15^a \bmod 63$ ($q = 128$)