Jedes Bit des ersten Registers wird mittels einer
Hadamard-Transformation auf
![]() gesetzt, um die Zahlen
gesetzt, um die Zahlen ![]() zu repräsentieren:
zu repräsentieren:
| (8) |
Für mehrere Bits ergibt sich somit
| (9) |
Dies läßt sich gut rekursiv implementieren:
| (10) |
Somit erhält man, wenn man diese Transformation auf ein
![]() anwendet
anwendet
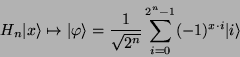 |
(11) |
(![]() bezeichne hier das Standardskalarprodukt über
bezeichne hier das Standardskalarprodukt über
![]() )
und unser Quantencomputer zur Faktorisierung ist nach der Anwendung
der Hadamard-Transformation nun in folgendem Zustand:
)
und unser Quantencomputer zur Faktorisierung ist nach der Anwendung
der Hadamard-Transformation nun in folgendem Zustand:
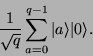 |
(12) |