Nächste Seite: Wieso ist dieses Verfahren Aufwärts: Details Vorherige Seite: Details Inhalt
Im folgenden nehmen wir an, daß der Punkt
![]() eine
Untergruppe der Ordnung
eine
Untergruppe der Ordnung ![]() erzeugt. Weiterhin sei
erzeugt. Weiterhin sei
![]() fest. Ferner notieren wir mit
fest. Ferner notieren wir mit ![]() einen lokalen
Parameter am Punkt
einen lokalen
Parameter am Punkt ![]() (dessen Koordinaten
(dessen Koordinaten ![]() seien, falls
seien, falls
![]() ). Wenn
). Wenn ![]() nicht die Ordnung
nicht die Ordnung ![]() besitzt und auch nicht
besitzt und auch nicht
![]() ist, dann sei
ist, dann sei ![]() . Falls
. Falls
![]() von Ordnung
von Ordnung
![]() ist (dann hat
ist (dann hat ![]() die Koordinaten
die Koordinaten ![]() ), dann sei
), dann sei ![]() .
Schließlich sei
.
Schließlich sei
![]() .
.
Abkürzend wird oft die Schreibweise
![]() (analog für
andere Funktionen) verwendet.
(analog für
andere Funktionen) verwendet.
Beweis: Sei
![]() die Bewertung am Punkt
die Bewertung am Punkt ![]() und
und
![]() . Setze nun
. Setze nun
![]() , wobei
, wobei ![]() regulär im
Punkt
regulär im
Punkt ![]() ,
, ![]() .
.
Zuerst betrachten wir den Fall, daß ![]() nicht im Divisor der Funktion
nicht im Divisor der Funktion
![]() ist, d.h.
ist, d.h. ![]() hat weder Ordnung
hat weder Ordnung ![]() noch gilt
noch gilt ![]() . Also ist
. Also ist
![]() . Die Funktion
. Die Funktion ![]() ist im Punkt
ist im Punkt ![]() regulär ([Sil86]). Dann ist
regulär ([Sil86]). Dann ist
![]() mit
mit
![]() .
.
Sei nun ![]() von Ordnung
von Ordnung ![]() , dann gilt
, dann gilt
Als letztes betrachten wir nun ![]() . Dann ist
. Dann ist
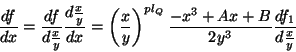
Sei nun
![]() . Wir wir gerade gesehen haben, ist
. Wir wir gerade gesehen haben, ist ![]() ein nichtnegativer Divisor, da aber andererseits
ein nichtnegativer Divisor, da aber andererseits
![]() , ist
, ist ![]() ein Hauptdivisor. Somit gilt
ein Hauptdivisor. Somit gilt ![]() und
die Behauptung ist bewiesen.fill
und
die Behauptung ist bewiesen.fill
![]()
Beweis: Zuerst zeigen wir, daß ![]() wohldefiniert ist. Seien
wohldefiniert ist. Seien ![]() linear äquivalente Divisoren. Also gibt es nach der Definition
von linearer Äquivalenz bei Divisoren (Def. 8) und
der Definition von Hauptdivisor (Def. 7) eine Funktion
linear äquivalente Divisoren. Also gibt es nach der Definition
von linearer Äquivalenz bei Divisoren (Def. 8) und
der Definition von Hauptdivisor (Def. 7) eine Funktion
![]() , so daß
, so daß
![]() . Wenn nun also
. Wenn nun also ![]() ,
dann ist
,
dann ist ![]() ; denn
; denn
Nun kann man immer ![]() rational über
rational über ![]() wählen und so erhält
man
wählen und so erhält
man
![]() , da
, da ![]() als Punkt der elliptischen Kurve
rational über
als Punkt der elliptischen Kurve
rational über ![]() ist.
ist.
Um nun zu zeigen, daß ![]() ein Homomorphismus ist, sei
ein Homomorphismus ist, sei
![]() und
und
![]() . Wir setzen außerdem
. Wir setzen außerdem
![]() . Nun ist
. Nun ist
Da ![]() auf
auf
![]() nicht verschwindet, ist es injektiv und somit
ein Monomorphismus. Die Konstruktion dieses Monomorphismus kann auch
aus einem allgemeinen Ergebnis von Serre ([Ser58, S. 40-41])
ableiten.fill
nicht verschwindet, ist es injektiv und somit
ein Monomorphismus. Die Konstruktion dieses Monomorphismus kann auch
aus einem allgemeinen Ergebnis von Serre ([Ser58, S. 40-41])
ableiten.fill
![]()
Stefan Röhrich stefan@roehri.ch