Wieso ist dieses Verfahren schnell?

Lemma 3   Sei $Q \in \langle P \rangle$. Dann kann man den Wert der Funktion $f'_Q/f_Q$ am Punkt $R$ mit $O(\ln p)$ Operationen in $\mathbbm{F}_q$ berechnen.

Beweis: Wir wählen uns $D_Q = (Q+S) - (S)$, wobei $S$ ein Punkt der Ordnung $2$ ist. Ferner notieren wir mit $\psi_k$ die Funktion, die durch

$$(\psi_k) = k (Q+S) - (kQ+S) - (k-1)(S)$$

definiert ist.

Es gilt

$$(\psi_p) = p (Q+S) - (pQ+S) - (p-1)(S) = p (Q+S) - (S) - (p-1)(S) = pD_Q$$

und somit ist $\psi_p = f_Q$ bis auf eine multiplikative Konstante.

Sei nun $k = k_1 + k_2, k_i \geq 0$. Nach [Sem93] gilt dann die folgende Gleichung

$$\psi_k \lambda_{k_1, k_2} = \psi_{k_1}\psi_{k_2} ,$$ (3)

wobei $\lambda_{k_1, k_2}$ eine Funktion ist, die

$$(\lambda_{k_1, k_2}) = (kQ+S) - (k_1Q+S) - (k_2Q+S) + (S)$$

erfüllt.

Gleichung (3) öffnet uns nun eine Methode zur Berechnung des Funktionswertes $f'_Q/f_Q(R)$. Aus (3) erhalten wir nämlich

$$\psi'_k/\psi_k = \psi'_{k_1}/\psi_{k_1} + \psi'_{k_2}/\psi_{k_2} - \lambda'_{k_1, k_2}/\lambda_{k_1, k_2}$$

und können somit die Funktion $\psi'_k/\psi_k$ durch eine Linearkombination von $O(\ln k)$ verschiedenen Funktionen der Form $\lambda'_{k_1, k_2}/\lambda_{k_1, k_2}$ ausdrücken. Zwar wird hier auf den ersten Blick ein Baum aufgebaut, der die Auswertung von $O(k)$ Funktionen erfordert, durch geeignete Wahl der $k_1, k_2$ ist es aber möglich, daß bei jeder weiteren Baumtiefe nur konstant viele neu auszuwertende Funktionen hinzukommen, somit kommt man auf $O(\ln k)$ Funktionsauswertungen.

Seien nun $\eta_{k_1,k_2}$ und $\kappa_k$ wie folgt definiert:

$$(\eta_{k_1,k_2}) = ((k_1+k_2)Q+S)+(-k_1Q+S)+(-k_2Q+S)-3(S),$$

$$(\kappa_k) = (kQ+S) + (-kQ+S) - 2(S),$$

wobei zu bemerken ist, daß $\eta_{k_1,k_2}(X-S)$ und $\kappa_{k_1}(X-S)$ lineare Funktionen in $x, y$ sind. Die Koeffizienten dieser Funktionen werden bestimmt durch die Koordinaten der Punkte $(k_1+k_2)Q$, $k_1Q$ und $k_2Q$.

Aus

$$\begin{eqnarray*} (\eta_{k_1,k_2} \kappa_{k_1}^{-1} \kappa_{k_2}^{-1}) & = & ((... ...S) \\ & = & (kQ+S)-(k_1Q+S)-(k_2Q+S)+(S) = (\lambda_{k_1, k_2}) \end{eqnarray*}$$

erhalten wir

$$\lambda_{k_1, k_2} = \eta_{k_1,k_2} \kappa_{k_1}^{-1} \kappa_{k_2}^{-1}$$

und man errechnet sich durch Anwendung der Derivationsrechenregeln

$$\begin{eqnarray*} \frac{\lambda'_{k_1, k_2}}{\lambda_{k_1, k_2}} & = & \left(\fr... ...ppa'_{k_1}}{\kappa_{k_1}} - \frac{\kappa'_{k_2}}{\kappa_{k_2}} . \end{eqnarray*}$$

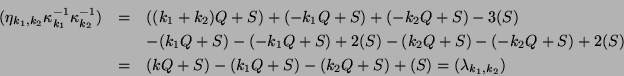
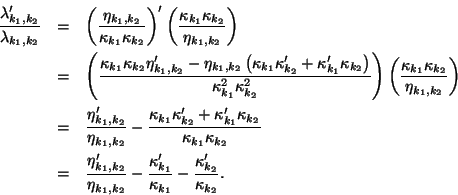
Die Funktionen der letzten Zeile dieser Gleichung können durch die folgenden Betrachtungen bestimmt werden. Sei $\delta = ax + by +c$ eine beliebige in $x, y$ lineare Funktion und $\delta_1 = \delta(X+S)$. Wir müssen den Wert der Funktion $\delta'_1/\delta_1$ an einem Punkt $R$ bestimmen und drücken dazu diese Funktion durch die Funktionen $delta$, $\delta'$ aus, wobei $\delta' = d\delta/dx = a + b(3x^2+A)/2y$ ($A$ aus der Definition der verwendeten elliptischen Kurve). Wir haben $d\delta = (2y\delta')(dx/2y)$ und wissen aus [Sil86, III. §5], daß $dx/2y$ ein invariantes Differential auf $E$ ist, d.h. $(dx/2y)(X+S) = (dx/2y)(X)$ für alle $S \in E$. Wenn wir nun $\delta_2=2y\delta'$ einführen, erhalten wir $d\delta(X+S)=\delta_2(X+S)(dx/2y)$ und so $\delta'_1=\delta_2(X+S)/2y$ und schließlich

$$\frac{\delta'_1}{\delta_1} = \frac{\delta_2(X+S)}{2y\delta(X+S)}.$$ (4)

Also müssen wir die Werte von $O(\ln k)$ Funktionen der Bauart $\delta'/\delta$ auswerten, deren Koeffizienten durch die Koordinaten der Punkte $(k_1+k_2)Q, k_1Q$ und $k_2Q$ bestimmt sind. Insgesamt haben wir $O(\ln k)$ solcher Punkte auszuwerten, da die Punkte dieser Menge durch dieselbe Menge ausgedrückt werden, ist die Komplexität dieser Berechnung nicht mehr als $O(\ln k)$ Operationen in $\mathbbm{F}_q$.

Aus (4) folgt außerdem, daß die Funktionen $\eta'_{k_1,k_2}/\eta_{k_1,k_2}$ und $\kappa'_{k_i}/\kappa_{k_i}$ an $R$ regulär sind. Also benötigt insgesamt die Komplexität der Auswertung der Funktionswerte $\psi'_k/\psi_k$ an $R$ nicht mehr als $O(\ln k)$ Operation in $\mathbbm{F}_q$. Genauer gesagt werden die obigen Berechnungen in einer Körpererweiterung von $\mathbbm{F}_q$ ausgeführt, die man durch Adjungation des Punktes der Ordnung $2$ erhält, aber da diese Erweiterung höchstens Grad $3$ hat, ist der Aufwand für diese Operationen proportional zu denen in $\mathbbm{F}_q$.fill

Aus Lemma 3 folgt, daß die Komplexität des diskreten Logarithmusproblems in der Gruppe $\langle P \rangle$ nicht mehr als $O(\ln p)$ Operationen in $\mathbbm{F}_q$ beträgt. Tatsächlich müssen wir, um $n$ zu erhalten, so daß $Q = nP$ in $E(\mathbbm{F}_q)$ gilt, die Werte $\phi(Q)$ und $\phi(P) \in \mathbbm{F}_q$ wie in Lemma 3 berechnen und daraus schließlich $n = \frac{\phi(Q)}{\phi(P)}$ durch Rechnung in $\mathbbm{F}_q$, womit wir dann den diskreten Logarithmus berechnet hätten.